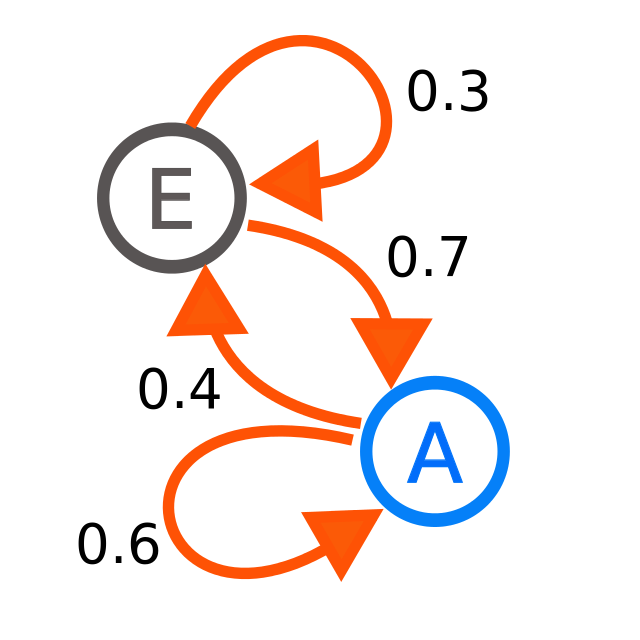
Markov chains are an important data science tool because they can be used to model and analyze complex systems as well as predict future states. They are particularly useful for analyzing data sequences such as text, video, audio, or other digital data. Markov chains can also be used to simulate a system’s behavior over time, which can help with decision-making, forecasting, and optimization.

What is the Markov chain used for in real life?

Markov chains are used to model a system’s behavior over time. They are used to forecast a system’s future states based on its recurrent state and the probabilities of state transitions. Markov chains can be used in a variety of fields, including economics, biology, genetics, computer science, and finance. They are also used in natural language processing to model languages, recognize speech, and generate text.

Natural language processing, speech recognition, financial analysis, predictive modeling, and bioinformatics are just a few of the real-world applications for Markov chains. Markov chains, for example, are commonly used in speech recognition to predict the likelihood of one word following another. They can be used in natural language processing to analyze large amounts of text data and identify patterns or relationships between words. Markov chains are frequently used in financial analysis to forecast stock market behavior based on past trends. Finally, Markov chains can be used in bioinformatics to analyze protein sequences and identify patterns that may indicate the function or evolutionary relationships.

What are Markov chains examples?

1. Text Generation: Markov chains can be used to generate new text by taking the existing text as input and generating a probability distribution of what words will appear next.

2. Image Captioning: Captions for images can be generated using Markov chains. The chain can determine what objects are in the image and suggest possible captions based on that information by analyzing the image.

3. Music Composition: Markov chains can also be used to compose music by generating a series of notes based on probabilities derived from existing music patterns.

4. Weather Forecasting: By analyzing past trends and creating probability distributions of potential outcomes, Markov chains can be used to forecast future weather events.

Is Markov chain irreducible?

Yes, Markov chains are irreducible. That is, given any two states in the chain, it is possible to transition between them in a finite number of steps.

Do Markov chains always converge?

Contrary to popular belief, they do not always converge. Markov property can either converge to a steady state or cycle between different states depending on the initial conditions.

When is a Markov chain periodic?

It is periodic if there is an integer n>1 such that after n steps, all states in the chain return to their original state matrix.

What is the Markov chain in probability?

They are a type of stochastic process model system transition between states. They are commonly used to describe random processes in probability and statistics. The probability of transitioning from one state to another in a stochastic is determined solely by the current state and not by any prior states. As a result, it is useful for modeling processes with no memory of the past, such as stock prices or weather patterns.

How to make a Markov chain model?

1. Determine which system you want to model.
2. Determine the system’s states and assign a numerical value to each.
3. Select transition probabilities that describe the likelihood of changing from one state to another.
4. Determine the system’s stationary distribution of states, which is a measure of the likelihood that any given state will be reached after a large number of possible state spaces.
5. Using this stationary distribution, multiply the initial probability by the stochastic matrix to calculate the probability of transitioning from one state of the Markov chain to a two-state markov.
6. Use these probabilities to simulate random state transitions and observe how they affect the system’s long-term behavior over time, such as expected values for certain variables.

How to simulate the Markov chain?

1. Define your Markov chain’s states and transitions: The states are the possible values of a random variable, and the transitions are the methods for moving from the present state.

2. Determine the transition probabilities: This is accomplished by constructing a transition probability matrix, which contains the probabilities of transitioning from the previous state.

3. Generate an initial state: This is usually done at random or based on prior knowledge.

4. Create a Markov chain trajectory by using a loop that generates the next state based on the recurrent state and its associated probabilistic. Record the current state and any other relevant information, such as time elapsed or other parameters, at each step.

5. Analyze the results: Depending on your goals, this could entail calculating statistics (e.g., expected time in certain states) or plotting visualizations (e.g., heatmaps and mathematical matrix).

Are Markov chains memoryless?

Yes, they have no memory. This means that the transition probabilities of a Markov chain monte carlo are determined solely by the current state and not by the preceding sequence of events.

How to plot Markov chain in python?

The NetworkX library can be used to plot a Markov chain in Python. NetworkX is a Python package for creating, manipulating, and studying complex networks’ structure, dynamics, and functions. You can use NetworkX to create a graph object, add nodes and edges, and then draw the graph with matplotlib. To plot a Markov process chain, you must first define the transition matrix, which is a matrix that describes the probability of changing state of the process. The graph can then be plotted using the NetworkX draw() function diagram matrix.

What is an irreducible Markov chain?

An irreducible Markov model is one in which any state can be reached from any other state in a finite number of steps in use of continuous time markov matrix. This means that it is not possible to be “trapped” in a specific state, and that any other state can be reached from any other state in a finite number of steps using the monte carlo method of aperiodic Markov chain.

Is Markov chain stationery?

Markov chains are, indeed, stationery. This means that the stationary distribution of the markov chain remain constant over time and the types of markov. In other words, the likelihood of transitioning from one stochastic model to next state depends on continous time markov not the hidden markov.

Is Markov chain machine learning?

Markov chains are not a type of machine learning. A Markov chain is a type of probabilistic model that predicts the likelihood of certain behaviors or outcomes based on the system’s chain is said to be the probability of moving mcmc or the theory of markov chains that sum to 1. two state markov process moves from one state to anoth